音程を表す「セント」の式を求める

半音は100セント、オクターブは1200セントになると聞いたことはないですか？それだけなら話は単純ですが、セントと周波数の関係となると途端に難しくなってきます。今回は「セント」を求める式をなるべく丁寧に書き下したいと思います。

今回のブログのゴールは、次の式を求めることです。

nはセント値、aとbは比較する音の周波数です。

セント値は単独で存在するのではなく、aとbの2つの音程が存在して初めて決まるという所がまずポイントですね。

試しにaとbに何か値を入れて計算してみましょう。

aは110ヘルツのAの音、bは2オクターブ上の440ヘルツとします(オクターブ上の音は周波数が倍になります)。

式①に代入すると

ここでlogの部分を考えます。

「log2の4」は2を何乗すると4になるか？という数です(答えは2乗ですね)。

計算を続けると

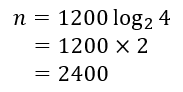
で2400セントとなりました。

1200セントで1オクターブなので、2400セントは2オクターブ上となります。

aとbに与えた周波数の関係と一致していますね。

セント値を求める式①は検索したらすぐに出てきます。

しかし、なぜそのような式になるのかの説明は見つかりませんでした。

logが出てくるなんて、ちょっと不思議な感じがしませんか？

以降は実際に式①を求めてみたいと思うので、興味のある方はぜひご覧下さい。

繰り返しになりますが、オクターブは1200セントということになっています。

周波数なら2倍でオクターブ上ですね。

では任意の数で使えるように一般化して、nセントとすると周波数は何倍になるでしょうか？

答えは2の1200分のn乗倍です。

言葉で書いても分かりにくいので式で表します！

周波数bが周波数aとnセント異なる時

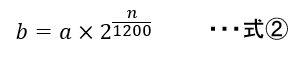
となります。

イメージが湧かないときはnに適当な値を代入してみて下さい。

例えばn=1200セントとすると

でbはaの2倍の(1オクターブ上の)周波数になります。

ではセントを求める式に変形していきます。

式②をn=の形にするということですね。

まずnが2の何乗の部分に乗っかっていて扱いづらいのので、底が2の対数を取ります。

この時点では「何やってるの？」と思われるかもしれませんが、もう少しお付き合い下さい・・。

logの中の掛け算は足し算に変換できます(何故か気になる方は証明を検索してみて下さい)。

こんな感じです。

log2のaを移項します。

logの引き算は割り算に変換できるので、式③の右辺は次のようになります。

また、式③の左辺はlogの定義から

従って式③は

両辺に1200を掛けて

ようやく最初の式①が出てきました！

数学の復習にもなって良い頭の体操になりましたね・・。

演奏には直接関係ない部分かもしれませんが、こういった考え方がチューナー等の機材を作るのに使われていると思うと興味深いです。

また機会があったら他の式の導出についても書いてみたいと思います。